Forecasting Future Demand Using Historic Trends
Modeling Methods: Demand Forecasting
Forecasting is an essential part of a company’s strategic planning. To respond proactively to market changes and business challenges, companies have to dedicate time to understand recent trends and forecast how things like demand, inventory, and customer engagement will develop over time. In part 1 and part 2 of this introduction to forecasting models, we’ll provide an example using statistical models and machine learning algorithms for time-series analysis. As an introduction to our forecasting methods, we will review the initial steps of forecasting including exploratory data analysis, checking for data stationarity, data transformations, and developing time-series models.
We’ve selected an example of product demand forecasting from Kaggle (a platform for sharing/exploring data science problems, and hosting real company projects often through paid competitions). In this example, a manufacturing company provided historic product demand for shipping projects to different regions throughout the world. Due to the time it takes to ship products, the company needs to predict demand for the next two months. This business case will be used to overview the major steps of our forecasting process.
Product Demand Business Case Data
A dataset was provided including product ids, warehouse ids, and product demand. For the purposes of our demonstration, we will simply be looking at total product demand. To do so, we sum the total order demand per month and use our models to forecast demand, one month at a time. Forecasting could also be performed by segmenting by warehouse and specific products, although the underlying concepts are the same. Our forecasting example also illustrates a univariate solution where we select a single variable, in this case “past orders”, to predict future order demand. Frequently multivariate predictions are needed to take into account other features which may impact order demand. Most of the same steps we review here will still apply although for multivariate models we might use alternative models such as VARMA (Vector Autoregressive Moving-Average. A statistical model based on acceptable values of residual activity) or ARIMAX (Auto Regressive Integrated Moving Average with Exogeneous Input).
Figure 1: Product table sample
Typically, there are several data cleaning steps to conduct and possibly data imputation to ensure we get the most out of our data. In this data, some of the product demands were entered with brackets which we removed. Otherwise, we didn’t have any missing data or other problems. If we had missing data, we could look at data imputation methods (which predict values that can be used for the missing data) such as multiple imputation by chained equations or use k-nearest neighbor models.
Exploratory Data Analysis (EDA)
Initial explorations into the nature of the data ensures we understand the data well before any modeling begins. At Northwestern Analytics, we work closely with our clients during this stage to understand where the data comes from, how it needs to be processed, and the type of features that can be used for modeling. In this example, the features are fairly straightforward, but when working on multivariate problems (i.e. using multiple features to make predictions) domain and business knowledge is an important part of selecting and designing model features.
A box-plot can be used to understand the range of orders for order demand. The plot in Figure 2 shows most of the data-points are below 1 mil., but we can see some of the orders are extremely right-skewed with several products exceeding 2 mil.
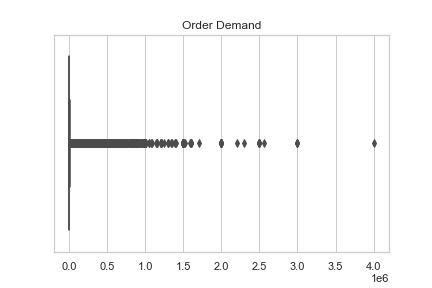
Figure 2: Order Demand Box Plot
We can also view these orders grouped by each category. While we will be predicting demand as a whole, we want to get an understanding of what we are working with. In Figure 3 we can see that Warehouse J has the most orders. By contrast Warehouse C typically has the largest quantity per order.
Figure 3: Warehouse demand
If we group observations monthly we can also see the total demand over time. (See Figure 4)
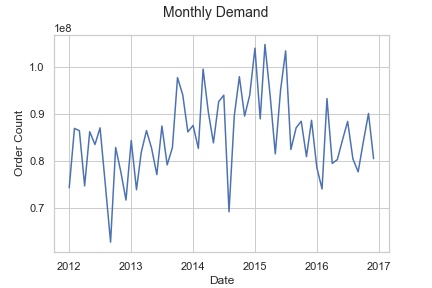
Figure 4: Summary statistics per warehouse
One of the most important things to determine during our initial explorations is whether the data is stationary or if there are underlying trends or seasonality within the data. Some statistical models require that we de-trend the data before we try to make predictions which, in part, is why a lot of work in time-series modeling is usually spent during this exploration phase.
To test if our data is stationary, we can perform the Augmented Dickey-Fuller (ADF) test. ADF is used to test the null hypothesis that the data is stationary. If the p-value is above .05 we reject the null hypothesis and treat the data as non-stationary. In the results below, the p-value is in fact above .05 so there may be some time-dependent trend or seasonality which we will need to remove from the data.
Order_Demand
Test statistic = -2.06
p-value = 0.26
Critical values:
1%: -3.551
5%: -2.914
10%: -2.595
Sometimes seasonality or trends can be seen easily by viewing the data. In Figure 5 we plot the monthly demand with a five month rolling average to help smooth the data. From the plot, it’s difficult to see any recurring cycles or seasonality, but we do see that the data trended up for some time before declining in more recent months.
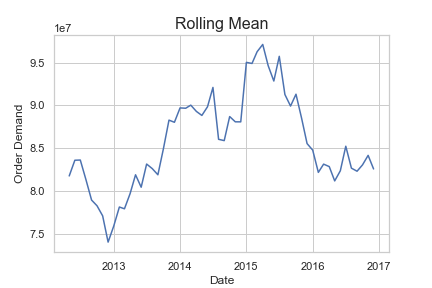
Figure 5: Order Demand rolling mean
Decomposition is another statistical technique we use to help separate out the seasonality and trend components of the data. Running decomposition on this data we do see the same trend in Figure 6. The seasonality component may be useful, but it’s difficult to know how much of the seasonality component is something we can rely on. Often if the seasonality component is complex, it’s due to random variation and isn’t as useful for making predictions. Lastly, the residuals don’t show any trend either in direction or in variability – suggesting we don’t have any trend or seasonality that seems more or less useful over time.
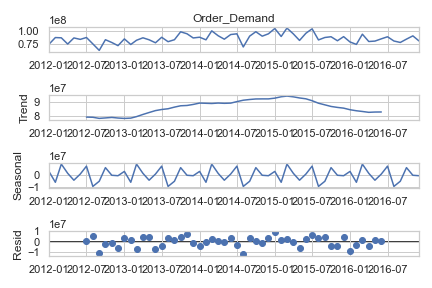
Figure 6: Decomposition
The determination of whether the data is stationary or non-stationary needs to be made before modeling begins. Some models, like ARIMA (Autoregressive Integrated Moving Average), require the data to be stationary. Others like Prophet and Holt-Winters don’t assume data stationarity and in fact decompose trend and seasonality similar to what we saw above. For our demonstration, we will try ARIMA and try to make our data stationary using a few common transformations. We try de-trending, differencing, simple weighted averages, and exponential smoothing. We won’t review each of the methods in detail, but what we want to check is whether the transformations remove our trends and pass the Dickey-Fuller test. Figure 7 plots the transformed data. We can immediately see the de-trended data doesn’t seem to have any obvious patterns. While the weighted moving average and simple exponential have done very little to remedy the existing trend.
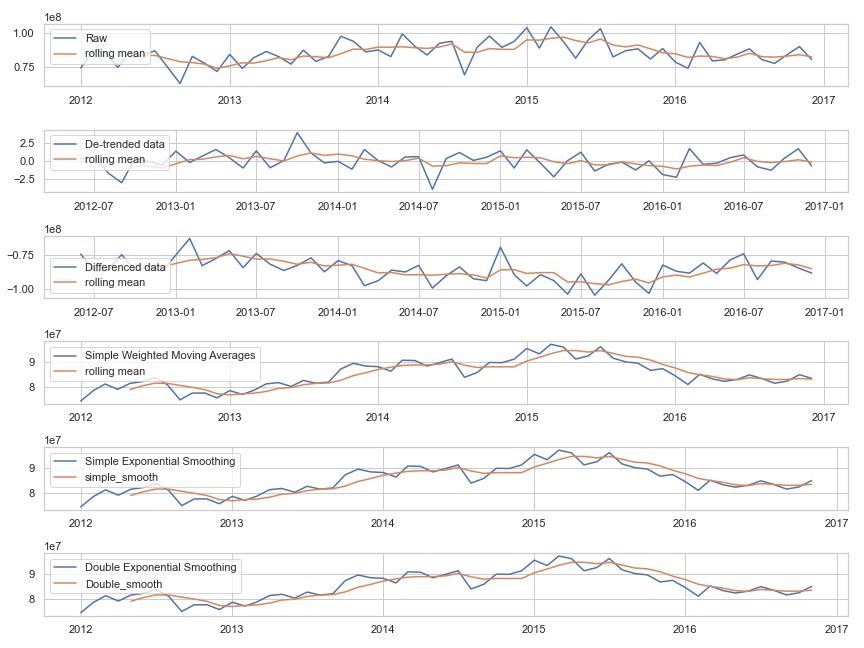
Figure 7: Transformed data
The Dickey-Fuller test is used to formally test whether the data is stationary. In this test, our null hypothesis is that the data is non-stationary. Typically we would reject the null hypothesis if the p-value is low, say < .1. However, since we are running multiple statistical tests, our p-value must be adjusted down since the more tests we run the more likely we are to get a low p-value by chance. Using the Bonferroni Correction, we would require a p-value below .02. However, we see that none of our transformations pass the test
Raw data
Test statistics = -2.1
p-value = 0.26
Critical values:
1%: -3.551
5%: -2.914
10%: -2.595
De-trend
Test statistics = -1.8
p-value = 0.37
Critical values:
1%: -3.558
5%: -2.917
10%: -2.596
De-trend with differencing
Test statistics = -1.9
p-value = 0.312
Critical values:
1%: -3.563
5%: -2.919
10%: -2.597
Simple weighted moving average
Test statistics = -2.2
p-value = 0.21
Critical values:
1%: -3.566
5%: -2.920
10%: -2.598
Simple_exp_smooth
Test statistics = -2.18
p-value = 0.213
Critical values:
1%: -3.568
5%: -2.921
10%: -2.599
Double exponential smoothing
Test statistic = -2.62
p-value = 0.089
Critical values:
1%: -3.568
5%: -2.921
10%: -2.599
Since none of our transformations have adequately de-trended the data, we fail to reject the null hypothesis that the data is non-stationary. We now have a few options. Since one of p-values is low at .0895, we could continue forward knowing we can’t be confident the model is stationary. Alternatively, we could try other data transformations, and our final option is to move on to models that don’t require the data to be stationary. For this article, we will complete the final steps of fitting an ARIMA model in order to outline the entire process. Moving forward we take our transformed data using double exponential smoothing as it returned the lowest p-value at .0896.
We can now review our transformed data using what are called Autocorrelation Functions (ACF) and Partial Autocorrelation Functions (PACF). This allows us to check whether the residuals (errors) are correlated with time series lags. For instance, if there was a cyclical trend every 3 months, we might see the data having high values at lag 3. In the plots in Figure 8, we see even with our transformed data, there are lags outside of the blue region of acceptable lag values. We have some correlations (see PACF) at lag 1, 4, 8, 9 and high lags after 12. However, the ARIMA forecasting model can help when the lag variables are not due to seasonality components. (In the case that lags are due to seasonality components and double exponential smoothing isn’t adequately detrending the data, this should become apparent in our final ACF and PACF charts after tuning the ARIMA parameters.)
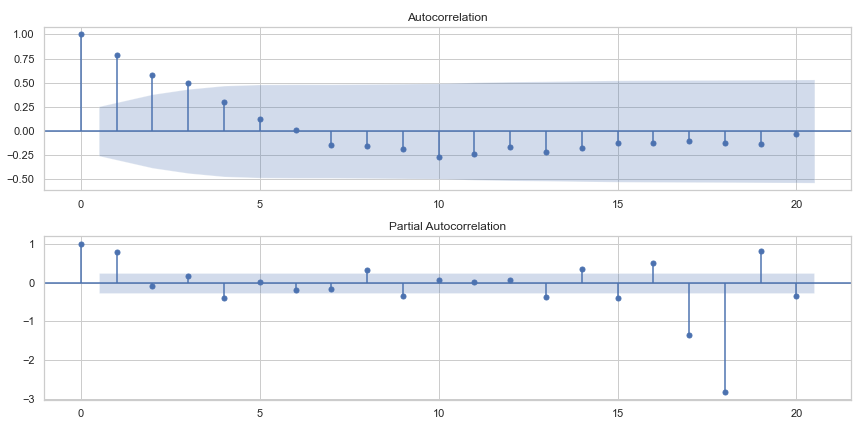
Figure 8: ACF and PACF plots
Modeling with ARIMA
We use ARIMA for this example, but in practice we would compare multiple forecasting models to determine what would work best for our data. Regardless of the model we train, we have to tune the model to our data. To do so, we need a training and validation set. In most cases, we will also hold out a final dataset to test the data after we’ve finished all our model tuning and changes. In our example, we train our data on the total monthly demand over a period of 50 months. Our validation set then covers another 10 months.
In our ARIMA model, we need to optimize for three parameters including auto-regressor, difference order and the moving-average. Selecting the best parameters is an iterative process which requires reviewing the PACF and ACF plots. We first want to optimize the differenced order parameter. To do so we look at the PACF and ACF plots we showed before and see if the lag 1 in the autocorrelation is zero or negative. If it is, we don’t need to increase the difference order parameter. If lag 1 was positive we could increase the difference order. In the case where we get very low correlations, we may need to reduce the difference order. Referring to our previous PACF and ACF plots, we have a positive lag, so we will increase the differenced order. We fit a model with a differenced order of 0 and 1 and review which model has a better fit. We can see that with ARIMA (0,1,0) (where 1 is the differenced order of 1), the model has a slightly improved performance with a lower AIC and BIC. In the plots in Figure 10 we also see the variance has decreased.
Figure 9: ARIMA model summary
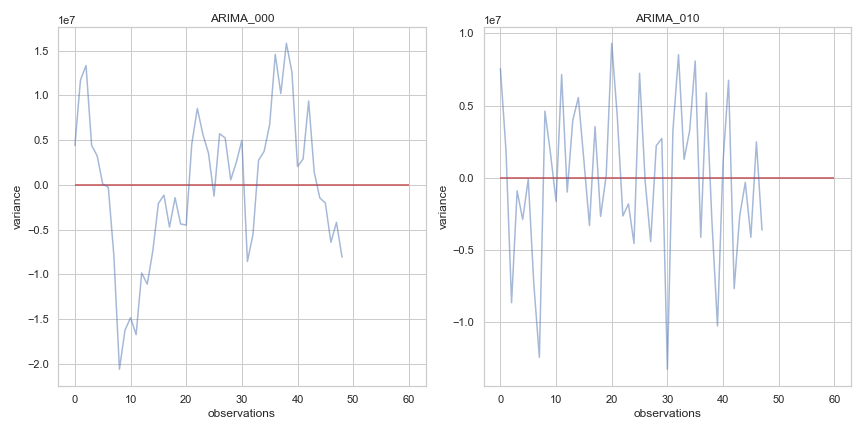
Figure 10: ARIMA 000 vs ARIMA 010
The next parameter we could adjust is the moving average order. However, we don’t see a negative value or sharp drop off at lag one so we don’t increase the order. The final parameter is the auto-regressor which we also don’t increase as we don’t have a negative lag 1.
Finally, we can view the PACF and ACF of the residuals again with our final model ARIMA (0, 1, 0). Our tuned ARIMA parameters have helped reduce the lag auto-correlations. However, there are still a few points outside the blue area which suggests we could look at seasonality components using models like SARIMA (Seasonal Autoregressive Integrated Moving Average) or Prophet (an additive model that fits non-linear trends with seasonality and holiday effects).
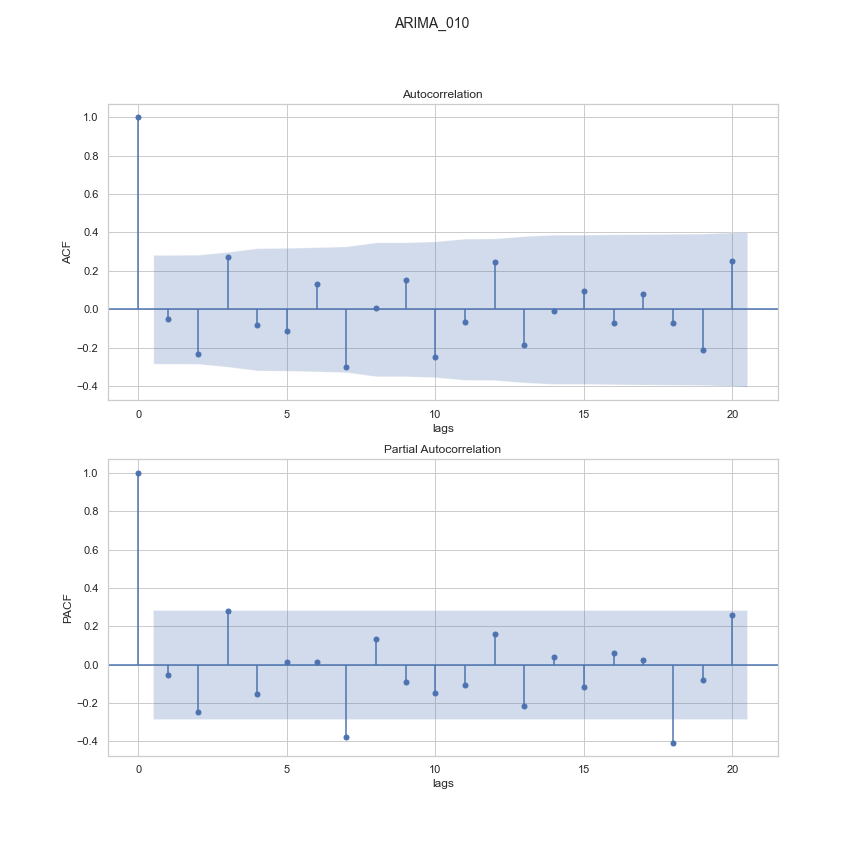
Figure 11: ARIMA ACF PACF plot
ARIMA Modeling Results
While we expect to find better performance looking at seasonality models, let’s review the ARIMA model predictions and see how we are doing. Since the company wants to make predictions two months into the future, our model makes two initial predictions using our training data. Rather than predicting the third month, we will add one more month of data to our model, refit the model, and make our next prediction and so on. This method of making predictions is called walk forward validation. For our demonstration, we held out a test set of ten months, so we can compare ten predictions on unseen data, just for this purpose. Following this method, the ARIMA model returns the results shown in Figure 12.
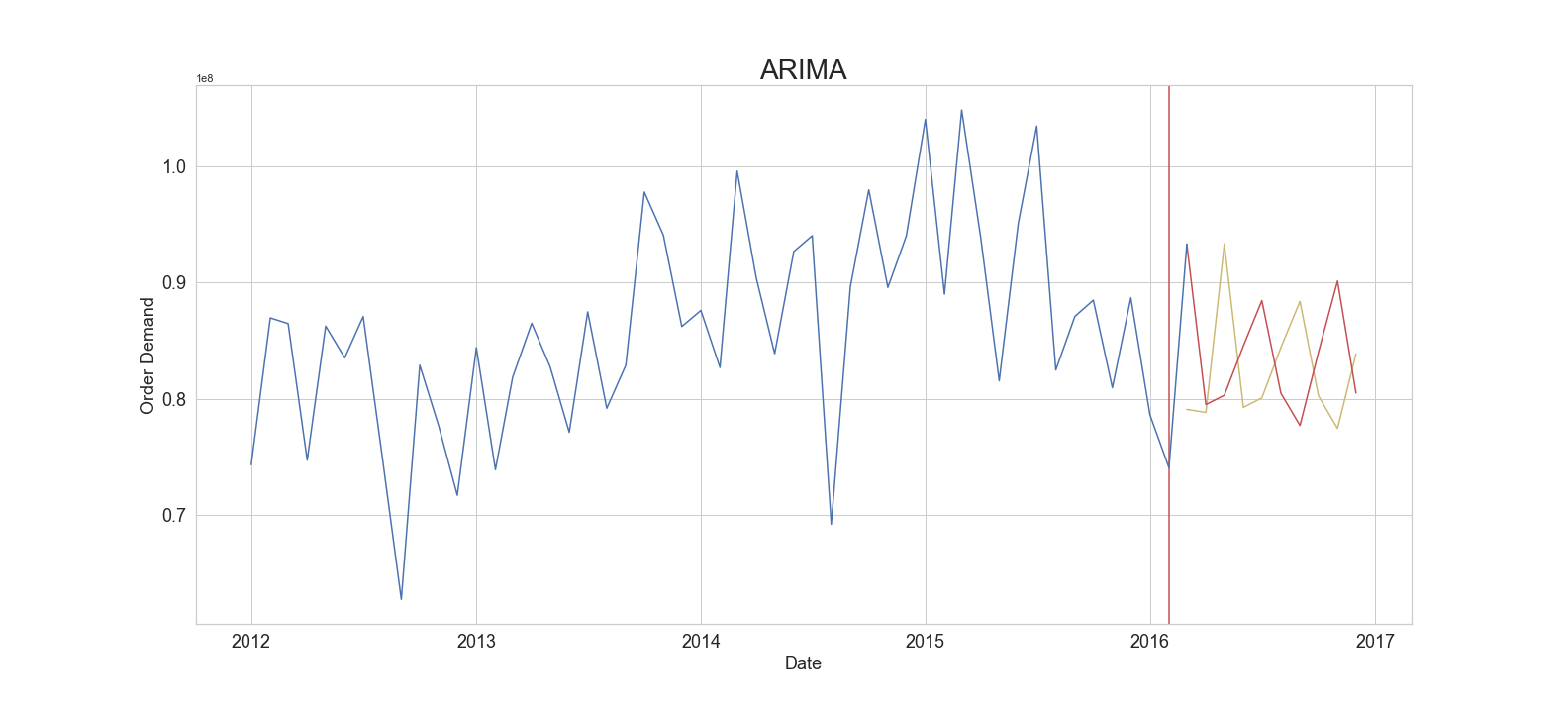
Figure 12: ARIMA forecasting result
A mean absolute percentage error (MAPE) means we are off on average by 8.9% of the target demand which isn’t great. We can see month to month our models predictions fluctuate and don’t coincide with the test data. As we expected, the ARIMA model isn’t well suited for our data and we may have seasonal components that need to be taken into account. However, we have a baseline to compare our seasonal models against and we’ve learned quite a bit about the nature of the data we’re working with.
This article provided an example of our process for time series forecasting. We’ve reviewed data cleaning steps and the exploratory phase of reviewing our data, including looking for any obvious patterns. We then reviewed whether our raw data was stationary and conducted data transformations which we again tested for stationarity. Next we selected data transformations and reviewed whether there were any autocorrelations using our PACF and ACF graphs. Using ARIMA, we attempted to account for the autocorrelations and again reviewed our PACF and ACF graphs which suggested there may be seasonality components. Finally, we fit our model to our data and compared our predictions to test data. In part 2, we will demonstrate the process of applying seasonal models including SARIMA, Prophet and Holt-Winters. For more information about how Northwestern Analytics helps clients through time series modeling see our Marketing and Customer Segmentation pratice.
-
Brennen Chadburnhttps://www.northwesternanalytics.com/author/brennen-chadburn/September 2, 2020
-
Brennen Chadburnhttps://www.northwesternanalytics.com/author/brennen-chadburn/November 16, 2020
-
Brennen Chadburnhttps://www.northwesternanalytics.com/author/brennen-chadburn/December 31, 2020
-
Brennen Chadburnhttps://www.northwesternanalytics.com/author/brennen-chadburn/September 16, 2022

















Excellent blog here!